We can classify all our approaches according to two points of view. On the one hand, "bottom-up" modeling approaches use the knowledge of biologists to build regulatory networks; different analysis techniques, based on mathematical expertise of the models, are then applied to these networks and integrated into associated software. On the other hand, "top-down" data mining approaches start from biological data produced on a large scale, represented in the form of very large interaction networks; the complexity of the latter requires the development of adapted mathematical and algorithmic tools for exploration and classification. These two points of view correspond respectively to the two themes presented below.
Discrete modeling of gene regulatory networks
Keywords: Boolean networks, graphs, discrete dynamical systems, Boolean functions
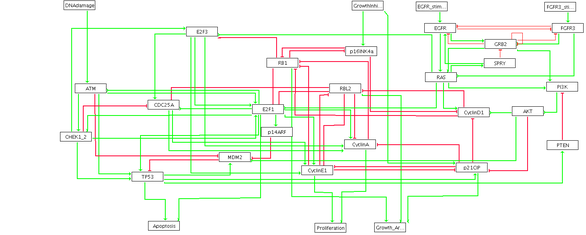
The modeling of regulatory networks aims at a mechanistic understanding of observed behaviors; it leads to simulations and predictions in biology. For this purpose, we use a qualitative formalism to represent interaction networks: the logical modeling. In this discrete formalism, a logical control graph is the data of a graph of interactions whose vertices are components, and of a family of parameters which determines the rules of cooperation between components interacting on a fixed component. A discrete dynamics is then defined, allowing to simulate the evolution of the states, defined by the discretized expression levels of the various components. From a mathematical point of view, in the Boolean case, it is a tool for analyzing the transformations of the set of vertices of a hypercube, the parameters defining the reciprocal influences of the coordinates.
The analysis of the dynamics of control networks consists in the study of attractors, basins of attraction, and more generally of the structure of the state transition graph. It quickly comes up against a problem of combinatorial explosion. A first strategy is to study techniques to reduce the number of components. We have proposed a method which, from a dynamic point of view, amounts to giving priority in terms of delay to the component, let's say to the "gene", which has been deleted. This procedure can be iterated, the only limitation being the self-regulated genes that cannot be reduced. By this method, we can ensure the preservation of some structures of the state transition graph, in particular the attractors (stable states and cyclic attractors). On the other hand, the trajectories are affected by this transformation, since the reduction amounts to pruning arcs of the transition graph. As a consequence, the method does not guarantee the conservation of reachability properties. Also, new complex attractors may appear, coming from non-terminal strongly connected components whose outgoing transitions have been removed. As a result, this reduction method brings out robust, and potentially biologically relevant, transient components in return.
A second strategy is to study the role in the dynamics of small, recurrent regulatory motifs whose function in biological networks is known. Their functional contexts are subspaces in which these motifs are the masters of the game: they behave there as when they are isolated. Thus, we first study their own dynamics. Then, the aim is to understand to what extent their local behaviors in their functional contexts contribute to the description of the global dynamics of the system.
To cope with the exponential explosion of the size of the graphs to be analyzed, the development of algorithms for the intelligent compaction of dynamic systems also plays an important role. Regardless of the difficulty of generating the state transition graph, it is also difficult to get a global view from an exploration of the trajectories. We have therefore built a graph giving a compressed view of the dynamics, which provides valuable information by highlighting the attractors, their basins of attraction, and certain transient properties. All these methodological developments are implemented in GINsim, a software dedicated to the modeling and analysis of logical control networks. We are in close contact with the developers of this software.
Analysis of large-scale interaction networks
Keywords: graphs, modularity, classification, communities, active modules, random walks, network embedding, dimension reduction
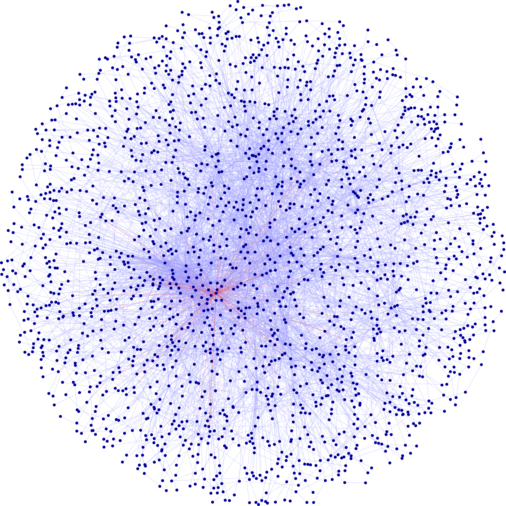
A second part of our work concerns the interaction networks that have been produced on a large scale since the advent of the post-genomic era and high-throughput screening techniques. These networks contain hundreds, even thousands of interactions between biological macromolecules. With the right tools, they offer the possibility of accessing an unprecedented amount of information on gene and protein functions at the cellular level.
Considering these large networks as simple undirected graphs, one way of approaching their analysis is to use combinatorial methods to search for partitions into communities; the communities obtained must then be analyzed so that they make sense in biology. In this context, we have developed various methods and tools. Several original algorithms allow to build overlapping or disjoint communities. Identifying the best partitioning of a graph is an intrinsically NP-hard problem. We have therefore developed several combinatorial optimization heuristics whose goal is to maximize a measure of the community structure of the graph. The chosen measure is the modularity criterion (Newman, 2006). One of these algorithms, an overlapping class partitioning method, has led to the identification of multifunctional proteins. Our tools are available online and widely used, among others, as applications within the international software Cytoscape dedicated to the study of these networks. We have also developed a bootstrap method in graph partitioning to give an indication of the robustness of the classes, as well as a functional enrichment approach based on the calculation of distances in the network.
We have adapted the definition of modularity to the simultaneous consideration of several networks sharing nodes, called multiplex networks. The aim is to integrate various points of view on the same set of proteins, reflecting the heterogeneous character of their interactions. We have applied this method to the detection of communities in simulated multiplex networks, modeled as independent realizations of different Stochastic Block Models (SBM) sharing the same latent community membership variables; the comparison of this approach to simple network aggregation highlights its efficiency. This work, whose ultimate goal is to define and annotate more finely functional modules of proteins, has been successfully applied to a multiplex network resulting from the simultaneous consideration of four biological networks.
Perspectives common to both research themes
Both approaches, bottom-up and top-down, give us different and complementary visions of cellular functioning. We are working to bring these two axes together, sharing among others the use of gene and protein expression data produced by transcriptomics and proteomics. In our projects, we use large-scale biological data to expand or parameterize Boolean models; conversely, large static networks are contextualized to make them more dynamic. The simultaneous consideration of these two scales of interactions leads us to develop new mathematical approaches, such as modeling the expressions of proteins in a large network of interactions via spatial models of the Markov field type.
Applications to biology
A very strong common objective, which is the raison d'être of our work, is to stay as close as possible to concrete applications in biology. This objective is achieved through collaborations that are often international, and that have already borne fruit through publications in high impact journals.
We studied a Boolean model of the regulatory network involved in bladder cancer and proposed an explanation for the co-occurring and mutually exclusive mutations observed in these cancers. A Boolean model also allowed us to predict synergies between anti-cancer drugs used in targeted therapy against gastric cancers. These predictions have been experimentally validated by our collaborators. We have also worked on functional prediction for proteins involved in cancers from large scale data (prostate cancer, gastric cancer), and on the study of relationships between human diseases through their comorbidities.
Other projects include the modeling of the iron/sulfur cluster homeostasis system in E. coli, and the study of hematopoietic stem cell differentiation and aging.
The specificity of each of these applications and their diversity make our tools evolve and new mathematical questions emerge.